Competition Progress
Catalog Problems Solved
0 problems completed
This week: 0 problems solved
USAPhO Track — F=ma Master Orientation
F=ma is a fast, algebra-based mechanics exam. Winning = clean models, free-body diagrams, and recognition of classic templates.
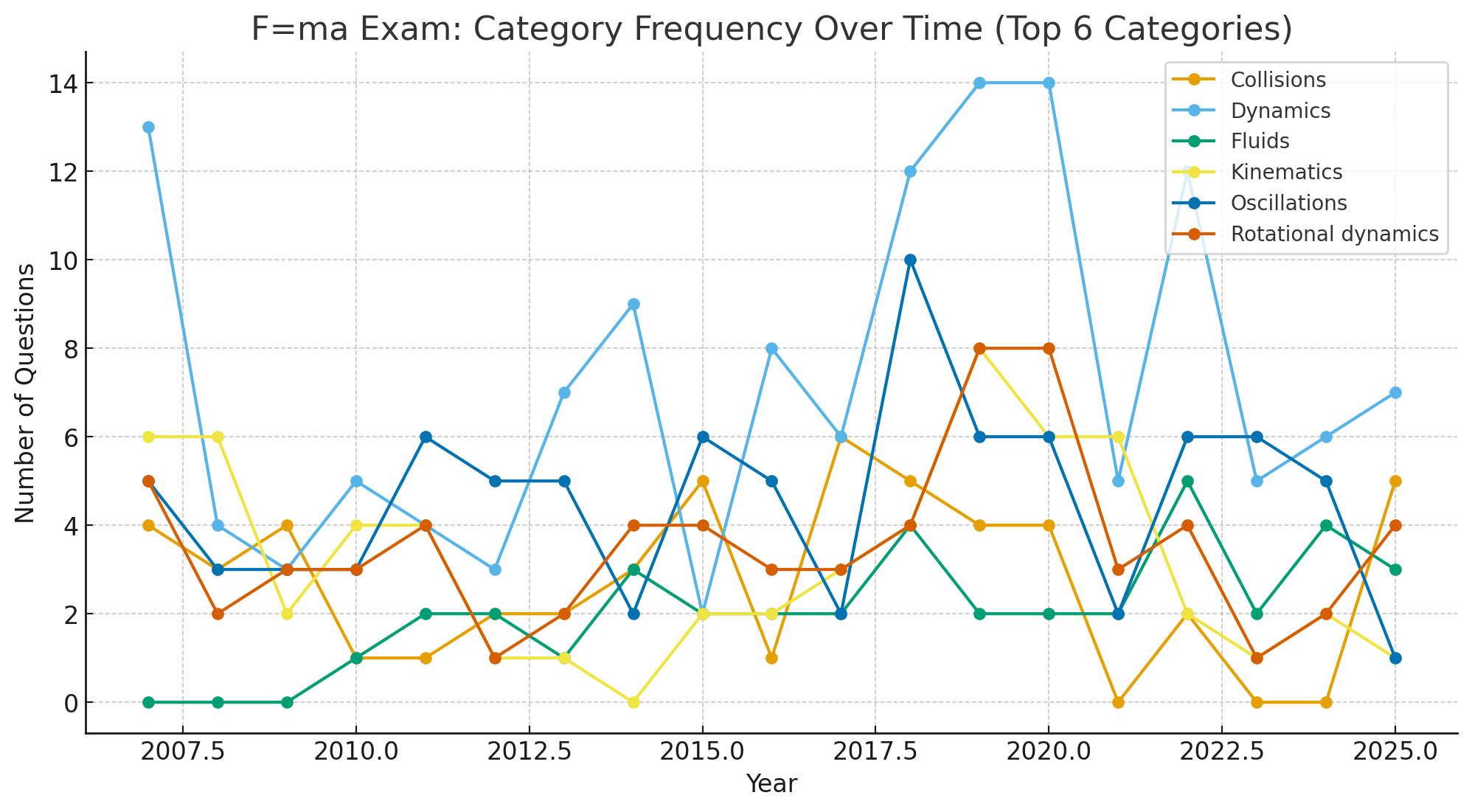
Dominant share (from your dataset):
Dynamics 27.3% (139) · Oscillations 17.1% (87) · Rotational 13.4% (68) · Kinematics 12.0% (61) — together ≈69.7% (N=509).
Dynamics 27.3% (139) · Oscillations 17.1% (87) · Rotational 13.4% (68) · Kinematics 12.0% (61) — together ≈69.7% (N=509).
Exam Basics
- Mechanics MCQ; ~75–90 min; usually no calculator.
- Aim ~70–80% raw; triage ruthlessly.
- Pipeline: diagram → laws (ΣF/energy/momentum/torque) → algebra → units → sanity.
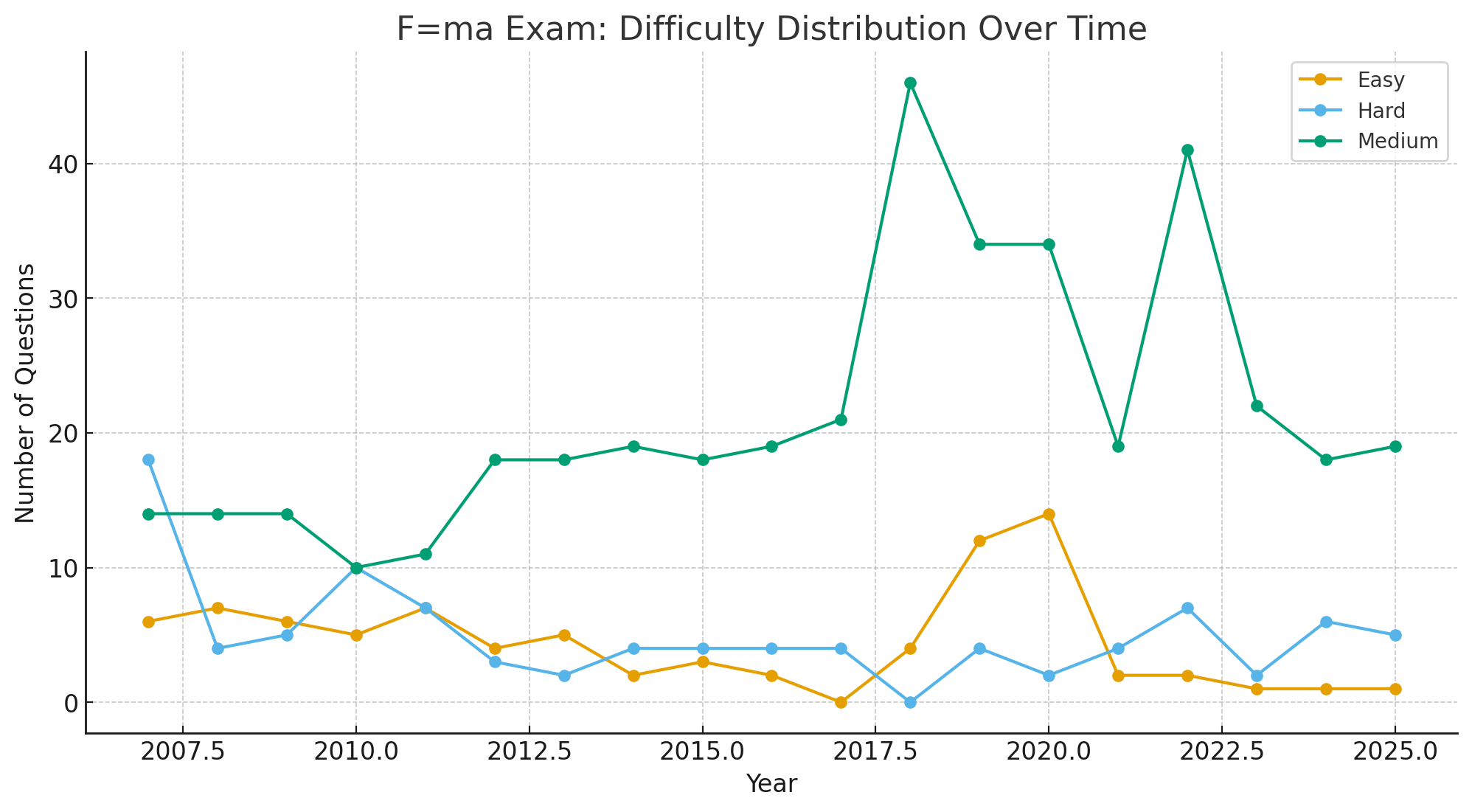
Difficulty Snapshot
- Dynamics mostly Medium; some Hard/Easy.
- Oscillations mostly Medium.
- Kinematics rich in Easy → start here.
- Collisions skew Hard; concept heavy.
Where the points are (Interactive)
2025 F=ma Exam Results (Official)
Participation
| Scored exams | 5848 |
| Date | Feb 12, 2025 |
Score Stats
| Min | 0 |
| Max | 25 |
| Median | 7 |
| Mean | 8.21 |
| Std. Dev. | 4.07 |
USAPhO Cutoff
| Cutoff | 15 |
| Invited (≥15) | 518 |
Prep tip: target 15+ correct (~60%). Lock Easy + familiar Medium first.
Historical Trends (2007–2025)
High-Yield Templates (Solve by Pattern)
Ballistic pendulum
- Hit: m v = (m+M) V (inelastic)
- Rise: ½(m+M)V² = (m+M) g h
- Trap: KE not conserved in the hit.
Rolling without slipping
- v = ωR, mgh = ½ m v² + ½ I ω²
- Solid sphere: I=⅖mR² → a=5g/7
Atwood / pulleys
- Consistent axes; rope constraints; shared tensions across segments.
Small-angle pendula
- Simple: T≈2π√(L/g) · Physical: T≈2π√(I/mgh)
- Constant force shifts equilibrium; period unchanged for Hooke/gravity.